|
Спирограф, если вы вдруг
не помните или не видели, выглядит так.
|
Не факт, что у всех, но у некоторых в детстве была игрушка под кодовым названием «Спирограф». Работала она так: в круг с зубцами внутри вставлялся ещё один круг, но с зубцами снаружи. После этого в дырочку второго круга можно было засунуть ручку или карандаш и катать им одну «шестерёнку» внутри другой, параллельно с тем любуясь получающимся узором. Узор представлял собой кривые, похожие на какие-то математические цветы. И в их регулярности наблюдалось особого рода очарование. Однако «аналоговый» вариант этой штуки, разумеется, страдал от заметного недостатка разнообразия: узоры, в общем-то, были довольно похожи друг на друга, а количество вариантов, хоть и было — при должном уровне изобретательности — довольно большим, но всё-таки маленьким. Всё, что можно получить на выходе, выучивалось довольно быстро. Тем не менее, сам метод способен подарить упорному экспериментатору очень много изящного и неожиданного. Особенно если от аналогового «спирографа» перейти к прогрессивному — цифровому.
Итак, как устроена эта штука. Одно колёсико катается внутри другого и некоторой своей точкой рисует траекторию. Та кривая, которая в данном случае рисуется синей точкой, называется «Гипоциклоида». Точнее, «гипоциклоидой» эта кривая бы называлась, если бы синяя точка совпадала с зелёной, а данный вариант называется «гипотрохоидой». Однако в дальнейшем всё равно будет использоваться иная модель построения этих кривых, поэтому пусть всё то, с чем мы дальше будем развлекаться, условно называется «гипоциклоидами».
Кстати, вот процесс в динамике.
Кстати, вот процесс в динамике.
Способ рисования «гипоциклоиды», которым мы сейчас воспользовались, отлично подходит для изготовления аналоговых устройств, рисующих такие кривые. Однако, как уже говорилось раньше, программные реализации дают больше вариантов, поэтому данный способ имеет смысл модифицировать.
Обратите внимание, центр зелёной окружности тоже движется по окружности, которую я нарисовал зелёным пунктиром. И одновременно с тем синяя точка тоже движется по синей пунктирной окружности. Иными словами, исходную систему можно преобразовать в более простую: центр окружности 2 движется по окружности 1, а по окружности 2 движется точка, оставляющая след.
Обратите внимание, центр зелёной окружности тоже движется по окружности, которую я нарисовал зелёным пунктиром. И одновременно с тем синяя точка тоже движется по синей пунктирной окружности. Иными словами, исходную систему можно преобразовать в более простую: центр окружности 2 движется по окружности 1, а по окружности 2 движется точка, оставляющая след.
Это намекает нам на то, что мы можем избавиться от некоторых ограничений «аналогового» варианта: в нём ведь соотношение количества оборотов центра зелёной окружности вокруг центра красной с количеством оборотов зелёной окружности вокруг своей оси диктовалось суровыми условиями аналоговой реальности.
Окружности ведь касаются друг друга зубчиками (невидимыми на чертеже), а потому проскальзывание невозможно. В результате, то расстояние, которое точка соприкосновения окружностей «проходит» по зелёной окружности, в точности равно тому, которое она проходит по красной. Соотношение количества оборотов, таким образом, определяется соотношением длин окружностей. Ну и соотношение «скоростей вращения» тоже определяется им же. Если, например, радиус зелёной окружности втрое меньше радиуса красной, то эта зелёная окружность при качении по красной успеет уложить свою длину в ней три раза.
Однако без аналогового девайса такая синхронизация теряет всякий смысл и вполне возможно задавать соотношение количества оборотов произвольным образом, что, разумеется, приведёт к увеличению разнообразия.
Наконец, можно сделать ещё более интересное: включить в систему не две окружности, а больше. По точно такому же принципу: по первой окружности ездит центр второй, по второй — центр третьей, и так далее. По последней же окружности из цепочки ездит та точка, которая оставляет за собой след и тем самым рисует для нас «гипоциклоиду n-ного порядка».
Однако без аналогового девайса такая синхронизация теряет всякий смысл и вполне возможно задавать соотношение количества оборотов произвольным образом, что, разумеется, приведёт к увеличению разнообразия.
Наконец, можно сделать ещё более интересное: включить в систему не две окружности, а больше. По точно такому же принципу: по первой окружности ездит центр второй, по второй — центр третьей, и так далее. По последней же окружности из цепочки ездит та точка, которая оставляет за собой след и тем самым рисует для нас «гипоциклоиду n-ного порядка».
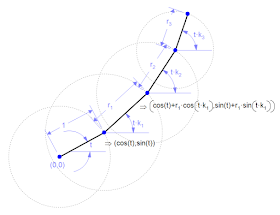
Формулу для фигур, построенных таким способом, найти довольно легко. Для простоты будем считать, что «главная» — «нулевая» окружность имеет единичный радиус и её центр расположен в начале координат.

Угол отклонения центра первой окружности от горизонтали назовём t.
Тогда координаты этого центра будут
Центр второй окружности находится на первой и в общем случае вращается с угловой скоростью, отличной от угловой скорости центра первой окружности. При помощи коэффициента k1 зададим эту пропорцию. Если центр первой окружности повёрнут на t, то центр второй будет повёрнут на k1*t. Ну и радиус первой окружности уже не равен единице, как у «главной нулевой». Назовём его r1.Для нахождения координат центра второй окружности надо к координатам центра первой окружности, вычисленным ранее, добавить аналогичным же способом найденные координаты смещения.
Ну и далее в том же духе, пока не доберёмся до нужного нам количества окружностей.
В конце концов у нас получится вот такая формула для гипоциклоиды третьего порядка.
Возможно, многие из читателей сейчас испытали растерянность, поскольку ранее видели только функции y(x), а тут y(t) и x(t). Однако проследите ещё раз за ходом мысли. t — это некий произвольный угол, для которого мы нашли координаты точки, рисующей кривую. Координат две, и обе зависят от угла. Меняя значения угла в некотором диапазоне, мы будем получать значения обеих координат и таким образом построим график.
Такой способ задания функций называется «параметрическим». И в данном случае он позволяет нам легко и непринуждённо запрограммировать построение кривых из подмножества гипоциклоид третьего порядка. Впрочем, по формуле видно, что любой порядок гипоциклоид получается вообще без напряга — просто методом тупого добавления совершенно идентичных по структуре слагаемых.
Однако если говорить именно о третьем порядке, то в данном случае точный вид кривой определяется шестью параметрами: тремя коэффициентами k и тремя радиусами окружностей.
Именно таким способом я и буду называть кривые: {k1, k2, k3, r1, r2, r3}.
Вот, например, кривая {5, −4, −5, 0.7, 1, 0.75}.
Такой способ задания функций называется «параметрическим». И в данном случае он позволяет нам легко и непринуждённо запрограммировать построение кривых из подмножества гипоциклоид третьего порядка. Впрочем, по формуле видно, что любой порядок гипоциклоид получается вообще без напряга — просто методом тупого добавления совершенно идентичных по структуре слагаемых.
Однако если говорить именно о третьем порядке, то в данном случае точный вид кривой определяется шестью параметрами: тремя коэффициентами k и тремя радиусами окружностей.
Именно таким способом я и буду называть кривые: {k1, k2, k3, r1, r2, r3}.
Вот, например, кривая {5, −4, −5, 0.7, 1, 0.75}.
Правда, я повернул её на 90°, чтобы усилить сходство с пальмовым листом.
Надо отметить, что разнообразие возможных форм поразительно велико. В ряде случаев даже тяжело поверить, что такая форма может быть получена этим вот хитрым вращением окружностей.
Надо отметить, что разнообразие возможных форм поразительно велико. В ряде случаев даже тяжело поверить, что такая форма может быть получена этим вот хитрым вращением окружностей.
Если один из радиусов сделать нулевым, то формула гипоциклоиды третьего порядка станет аналогична формуле гипоциклоиды второго. Таким образом, гипоциклоиды третьего порядка включают в себя как подмножество все гипоциклоиды первого и второго порядков.
Иными словами, картинки из спирографа с их помощью тоже можно рисовать.
Изображённая выше «бубна» являет собой один из классических видов гипоциклоид первого порядка. Тем не менее, человеку интуитивно кажется, что вращение двух окружностей никак не может дать что-то, столь похожее на квадрат. Прямые линии из двух кругов? Да вы бредите, господа!
Однако можно подобрать параметры, которые дадут в результате нечто, ещё более напоминающее прямые линии и составленные из них фигуры. Да-да, при помощи довольно простой системы шестерёнок действительно можно сделать девайс, который будет рисовать квадраты с несколько сглаженными углами.
Однако можно подобрать параметры, которые дадут в результате нечто, ещё более напоминающее прямые линии и составленные из них фигуры. Да-да, при помощи довольно простой системы шестерёнок действительно можно сделать девайс, который будет рисовать квадраты с несколько сглаженными углами.
Кстати, сами шестерёнки тоже можно нарисовать таким способом. Хотя, быть может, вам снова не верится, что так вообще может быть.
Однако да, может. Причём у этой фигуры есть своя собственная формула, как и у всех предыдущих. Причём сам вид формулы — один и тот же: меняются только коэффициенты.
Однако да, может. Причём у этой фигуры есть своя собственная формула, как и у всех предыдущих. Причём сам вид формулы — один и тот же: меняются только коэффициенты.
И тут, наверно, уже пора сказать, почему статья называется «Формула утки». Хотя многие наверно уже и так догадались: да, при помощи этого способа правда можно подобрать кривую, которая напоминает силуэт утки, вид сверху.
Поскольку же нам известны и общий вид формулы, и коэффициенты, мы имеем возможность получить точную формулу утки. Вот она:
Орнитологи теперь могут спать спокойно, а мы взглянем на ещё некоторое количество занимательных кривых.
Изящные математические цветы.
Изящные математические цветы.
Не уверен, но что-то вроде скелетов радиолярий.
Взрыв и ананас.
Генерал и грустный человек с бакенбардами.
Медальон и указатель «мирный атом вон там».
Два каких-то логотипа. Подозреваю, математико-сатанинских сект.
Желающие самостоятельно поэкспериментировать с гипоциклоидами третьего порядка могут скачать веб-приложение.
Вдобавок можно взять вариант с анимацией построения.
Лекс Кравецкий