Ни для кого не секрет, что многие из нас не слишком любят математику и геометрию, и что они зачастую слишком сложны. Но даже в этом случае может быть довольно ошеломляюще оглянуться назад в историю и обнаружить древних мыслителей, которые намного опередили свое время и придумали сложные теоремы, инновации и открытия в области математики. Одним из таких пионеров научной мысли является Евклид, древнегреческий математик, который процветал около 300 г. до н. э. и считается отцом геометрии.
Он родился в Александрии (Египет), его жизнь и наследие на протяжении веков стали предметом восхищения и почитания ученых. Более того, его важнейшая работа «Начала» не только заложила основу изучения геометрии, но и оказала глубокое влияние на развитие математики в целом. Давайте узнаем больше об этом человеке, опередившем свое время.
Другая интересная возможность заключается в том, что на образование Евклида повлияла пифагорейская школа мысли. Пифагорейцы, известные своим увлечением геометрией и математическим мистицизмом, оказали глубокое влияние на интеллектуальную среду Древней Греции. Акцент Евклида на геометрической абстракции и строгом доказательстве может отражать склонность Пифагора к математической чистоте и логическому выводу. Независимо от специфики его формального образования, очевидно, что Евклид вышел из этого горнила интеллектуального обучения с глубоким пониманием силы дедуктивного рассуждения и логической аргументации. Его математическое мастерство и педагогическая проницательность позже нашли выражение в его выдающемся произведении «Элементы», свидетельствующем о его мастерстве в геометрии и его способности превращать сложные математические концепции в элегантные логические доказательства.
В отсутствие конкретных биографических подробностей нам остается только размышлять о влияниях, которые сформировали раннюю жизнь и образование Евклида. Был ли он природным талантом? Или его вдохновляли великие люди, которые были до него? Как бы то ни было, вне сомнений остается непреходящее наследие его математического гения, которое продолжает вызывать трепет и восхищение у математиков и ученых по сей день. Путешествие Евклида из безвестности древних времен в священные залы математического бессмертия в современную научную эпоху служит свидетельством силы человеческого интеллекта и вечного поиска знаний и понимания.
Геометрия возникла органически в результате наблюдения и манипулирования физическими объектами в мире природы. Древние цивилизации, такие как египтяне и вавилоняне, разработали элементарные геометрические концепции для облегчения таких задач, как измерение границ суши, строительство зданий и предсказание небесных событий. Эти ранние геометрические принципы заложили основу для более абстрактного и систематического подхода к геометрии, который позже возник в Древней Греции.
Греческое понятие «геометрия», означающее «измерение земли» или «геодезия», отражает практическое происхождение геометрии в измерении и разделении земли. Однако именно греческие философы и математики стремились превратить геометрию из утилитарного ремесла в строгое интеллектуальное занятие. Фалесу Милетскому , которого часто считают первым математиком, приписывают введение в геометрию дедуктивного рассуждения и математической абстракции. Его теорема о свойствах треугольников, образованных пересекающимися прямыми, заложила основу для последующих геометрических исследований. Пифагорейцы, последователи философа Пифагора , еще больше продвинули изучение геометрии, наполнив ее чувством математического мистицизма и философской значимости. Теорема Пифагора, связывающая длины сторон прямоугольного треугольника, остается одним из самых известных результатов в геометрии и свидетельством силы математических рассуждений.
Однако именно Евклид систематизировал и систематизировал разрозненные геометрические принципы своих предшественников в единую систему, известную как «евклидова геометрия». Его выдающееся произведение «Элементы» служило исчерпывающим учебником по геометрии на протяжении более двух тысячелетий, обеспечивая строгую основу для изучения геометрических принципов, теорем и доказательств. Аксиоматический подход Евклида к геометрии, который опирался на небольшой набор самоочевидных истин, известных как аксиомы, заложил основу для дедуктивного метода, который впоследствии стал отличительной чертой математических рассуждений. Организовав геометрические понятия в логическую и иерархическую структуру, Евклид утвердил геометрию как дисциплину, основанную на строгих доказательствах и логической аргументации. Рождение геометрии представляет собой триумф человеческого интеллекта и любопытства, превративший практические заботы древних цивилизаций во вневременное интеллектуальное занятие.
«Начала» Евклида известны своей систематической организацией, логической строгостью и упором на дедуктивные рассуждения. Каждое предложение формулируется ясно и точно, после чего следует строгое доказательство, опирающееся на ранее установленные результаты. Аксиоматический метод Евклида, который начинается с небольшого набора самоочевидных истин и приводит к дальнейшим результатам посредством логической дедукции, устанавливает стандарт математического изложения. Влияние великого произведения Евклида выходит далеко за рамки геометрии, определяя ход математических исследований на протяжении веков. Его акцент на логических рассуждениях, строгих доказательствах и систематической организации служит моделью для математического изложения в различных областях, от алгебры и теории чисел до исчисления и за его пределами.
Его влияние можно также увидеть в развитии алгебраических методов. Его работа над пропорциями и соотношениями заложила основу для алгебраических рассуждений, особенно в контексте решения уравнений и манипулирования алгебраическими выражениями. Евклидова геометрия дала геометрическую интерпретацию алгебраических понятий, а его акцент на логических рассуждениях и строгих доказательствах заложил основу для развития современных алгебраических структур и методов.
Кроме того, он также внес значительный вклад в теорию чисел, особенно в теорию простых чисел. Книга VII «Элементов» посвящена изучению теории чисел, в том числе свойств простых чисел, делимости и алгоритма нахождения наибольшего общего делителя. Алгоритм Евклида для нахождения наибольшего общего делителя двух чисел остается фундаментальным инструментом в теории чисел и имеет приложения в таких областях, как криптография и информатика.
Он родился в Александрии (Египет), его жизнь и наследие на протяжении веков стали предметом восхищения и почитания ученых. Более того, его важнейшая работа «Начала» не только заложила основу изучения геометрии, но и оказала глубокое влияние на развитие математики в целом. Давайте узнаем больше об этом человеке, опередившем свое время.
Евклид: отец геометрии
🔹 Евклид заложил основы современной геометрии
Ранняя жизнь и образование Евклида не очень хорошо задокументированы, поэтому историкам приходится собирать воедино фрагменты свидетельств и предположений, чтобы составить портрет человека, стоящего за математической легендой. Хотя точные детали ускользают от нас, предположения и умозаключения дают заманчивое представление о годах его становления. Современные историки в целом сходятся во мнении, что Евклид получил образование в Академии в Афинах, интеллектуальном эпицентре древнего мира. Именно в этом оживленном городе процветали философские и математические идеи таких светил, как Платон и его последователи. Некоторые источники предполагают, что Евклид, возможно, был студентом Академии Платона или учился у учеников Платона, впитав философские основы, которые позже легли в основу его математических усилий.Другая интересная возможность заключается в том, что на образование Евклида повлияла пифагорейская школа мысли. Пифагорейцы, известные своим увлечением геометрией и математическим мистицизмом, оказали глубокое влияние на интеллектуальную среду Древней Греции. Акцент Евклида на геометрической абстракции и строгом доказательстве может отражать склонность Пифагора к математической чистоте и логическому выводу. Независимо от специфики его формального образования, очевидно, что Евклид вышел из этого горнила интеллектуального обучения с глубоким пониманием силы дедуктивного рассуждения и логической аргументации. Его математическое мастерство и педагогическая проницательность позже нашли выражение в его выдающемся произведении «Элементы», свидетельствующем о его мастерстве в геометрии и его способности превращать сложные математические концепции в элегантные логические доказательства.
В отсутствие конкретных биографических подробностей нам остается только размышлять о влияниях, которые сформировали раннюю жизнь и образование Евклида. Был ли он природным талантом? Или его вдохновляли великие люди, которые были до него? Как бы то ни было, вне сомнений остается непреходящее наследие его математического гения, которое продолжает вызывать трепет и восхищение у математиков и ученых по сей день. Путешествие Евклида из безвестности древних времен в священные залы математического бессмертия в современную научную эпоху служит свидетельством силы человеческого интеллекта и вечного поиска знаний и понимания.
🔹 Евклид и рождение геометрии
Рождение геометрии представляет собой поворотный момент в эволюции человеческой цивилизации, знаменующий начало систематических исследований свойств пространства, формы и формы. Хотя истоки геометрии можно проследить до практических потребностей древних обществ, таких как землемерие и архитектурное проектирование, ее формализация как математической дисциплины во многом обязана интеллектуальным усилиям древнегреческих ученых, таких как Фалес, Пифагор и, что особенно важно.Геометрия возникла органически в результате наблюдения и манипулирования физическими объектами в мире природы. Древние цивилизации, такие как египтяне и вавилоняне, разработали элементарные геометрические концепции для облегчения таких задач, как измерение границ суши, строительство зданий и предсказание небесных событий. Эти ранние геометрические принципы заложили основу для более абстрактного и систематического подхода к геометрии, который позже возник в Древней Греции.
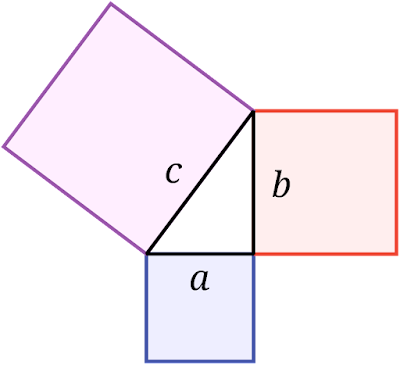
Греческое понятие «геометрия», означающее «измерение земли» или «геодезия», отражает практическое происхождение геометрии в измерении и разделении земли. Однако именно греческие философы и математики стремились превратить геометрию из утилитарного ремесла в строгое интеллектуальное занятие. Фалесу Милетскому , которого часто считают первым математиком, приписывают введение в геометрию дедуктивного рассуждения и математической абстракции. Его теорема о свойствах треугольников, образованных пересекающимися прямыми, заложила основу для последующих геометрических исследований. Пифагорейцы, последователи философа Пифагора , еще больше продвинули изучение геометрии, наполнив ее чувством математического мистицизма и философской значимости. Теорема Пифагора, связывающая длины сторон прямоугольного треугольника, остается одним из самых известных результатов в геометрии и свидетельством силы математических рассуждений.
Однако именно Евклид систематизировал и систематизировал разрозненные геометрические принципы своих предшественников в единую систему, известную как «евклидова геометрия». Его выдающееся произведение «Элементы» служило исчерпывающим учебником по геометрии на протяжении более двух тысячелетий, обеспечивая строгую основу для изучения геометрических принципов, теорем и доказательств. Аксиоматический подход Евклида к геометрии, который опирался на небольшой набор самоочевидных истин, известных как аксиомы, заложил основу для дедуктивного метода, который впоследствии стал отличительной чертой математических рассуждений. Организовав геометрические понятия в логическую и иерархическую структуру, Евклид утвердил геометрию как дисциплину, основанную на строгих доказательствах и логической аргументации. Рождение геометрии представляет собой триумф человеческого интеллекта и любопытства, превративший практические заботы древних цивилизаций во вневременное интеллектуальное занятие.
🔹 Человек, выгравировавший свое имя в истории
Фундаментальным шедевром Евклида является книга «Начала», трактат из тринадцати книг и его выдающееся произведение. Это было монументальное достижение в истории математики, служившее типичным учебником по геометрии на протяжении более двух тысячелетий. Трактат тщательно излагает основы евклидовой геометрии и устанавливает стандарты математического изложения, логических рассуждений и строгих доказательств. Тринадцать книг следующие:- Книга I – Основы плоской геометрии:
- Книга II - Геометрическая алгебра:
- Книга III - Свойства кругов:
- Книга IV - Правильные многогранники:
- Книга V - Теория отношений:
- Книга VI - Подобные фигуры:
- Книга VII - Теория чисел:
- Книга VIII - Арифметические и геометрические прогрессии:
- Книга IX. Продолжение теории чисел.
- Книга X - Иррациональные числа и геометрическая алгебра:
- Книга XI - Твердая геометрия:
- Книга XII - Додекаэдр и его свойства:
- Книга XIII - Метод Архимеда:
«Начала» Евклида известны своей систематической организацией, логической строгостью и упором на дедуктивные рассуждения. Каждое предложение формулируется ясно и точно, после чего следует строгое доказательство, опирающееся на ранее установленные результаты. Аксиоматический метод Евклида, который начинается с небольшого набора самоочевидных истин и приводит к дальнейшим результатам посредством логической дедукции, устанавливает стандарт математического изложения. Влияние великого произведения Евклида выходит далеко за рамки геометрии, определяя ход математических исследований на протяжении веков. Его акцент на логических рассуждениях, строгих доказательствах и систематической организации служит моделью для математического изложения в различных областях, от алгебры и теории чисел до исчисления и за его пределами.
🔹 На столетия впереди своего времени
Вклад Евклида в математику выходит далеко за рамки геометрии, охватывая широкий спектр математических дисциплин и закладывая основу для многих фундаментальных концепций и методов, которые продолжают формировать эту область и по сей день. Хотя он наиболее известен своими работами в области геометрии, особенно своим выдающимся произведением, влияние Евклида выходит за рамки этой единственной дисциплины, затрагивая теорию чисел, алгебру и математическую логику. Например, «Начала» Евклида представили аксиоматический метод математических исследований, заложив основу дедуктивного подхода, который впоследствии стал отличительной чертой математических рассуждений. Начав с набора аксиом или самоочевидных истин и получив дальнейшие результаты посредством логической дедукции, Евклид установил строгую основу для математических доказательств, которая продолжает влиять на эту область и по сей день. Аксиоматический метод дает прочную основу для построения математических теорий и обеспечивает ясность и точность математических рассуждений.Его влияние можно также увидеть в развитии алгебраических методов. Его работа над пропорциями и соотношениями заложила основу для алгебраических рассуждений, особенно в контексте решения уравнений и манипулирования алгебраическими выражениями. Евклидова геометрия дала геометрическую интерпретацию алгебраических понятий, а его акцент на логических рассуждениях и строгих доказательствах заложил основу для развития современных алгебраических структур и методов.
Кроме того, он также внес значительный вклад в теорию чисел, особенно в теорию простых чисел. Книга VII «Элементов» посвящена изучению теории чисел, в том числе свойств простых чисел, делимости и алгоритма нахождения наибольшего общего делителя. Алгоритм Евклида для нахождения наибольшего общего делителя двух чисел остается фундаментальным инструментом в теории чисел и имеет приложения в таких областях, как криптография и информатика.
🔹 Любимец студентов по всему миру
В конце концов, просто невероятно, как вклад одного человека в математику оказал глубокое и продолжительное влияние на эту область, формируя ход математических исследований на протяжении веков. Акцент Евклида на логических рассуждениях, строгих доказательствах и систематической организации установил стандарт математического изложения и заложил основу для многих фундаментальных концепций и методов математики. Наследие Евклида, от его аксиоматического метода до его понимания геометрии, теории чисел и алгебры, продолжает вдохновлять и информировать математиков и ученых по сей день, напоминая нам о вечной красоте и элегантности математической истины.(Copyrighted © Перевод с англ. Louiza Smith)
Источник:
By Aleksa Vučković,
«Euclid and the Birth of Geometry»