Правило Леонардо

Грациозный ствол дерева разделяется на ветви, сперва немногочисленные и мощные, а те — на все более тонкие. Это так прекрасно и так естественно, что вряд ли кто-нибудь из нас обращал внимание на простую закономерность. Дело в том, что общая толщина ветвей на определенной высоте всегда равна толщине ствола.

Этот факт уже 500 лет назад заметил Леонардо Да Винчи, который, как известно, был очень наблюдательным. Взаимосвязь получила название «Правило Леонардо» и долгое время никто не мог понять, почему так происходит.

В 2011-м году физик Кристоф Эллой из Калифорнийского университета предложил собственное любопытное объяснение.

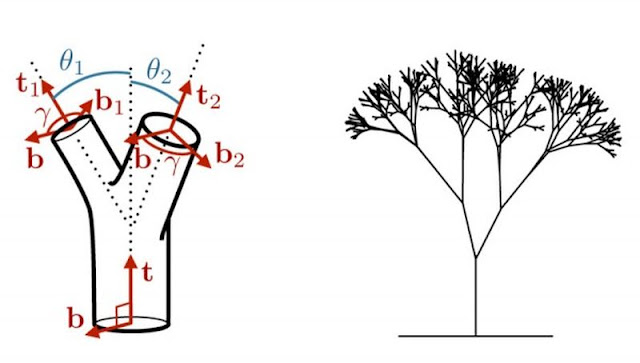
«Правило Леонардо» справедливо практически для всех известных видов деревьев. О нем осведомлены и создатели компьютерных игр, создающие реалистичные трехмерные модели деревьев. Более точно, правило это устанавливает, что в месте, где ствол или ветвь раздваивается, сумма сечений раздвоенных веток будет равна сечению исходной ветви. Когда затем и эта ветка раздвоится, сумма сечений уже четырех ее ответвлений будет по-прежнему равна сечению исходного ствола. И так далее.

Еще изящнее это правило записывается математически. Если ствол диаметром D разделяется на произвольное число ветвей n с диаметрами d1, d2 и так далее, сумма их диаметров, возведенных в квадрат, будет равна квадрату диаметра ствола. По формуле: D2 = ∑di2, где i = 1, 2, … n. В реальной жизни степень не всегда строго равна двум и может варьировать в пределах 1,8−2,3, в зависимости от особенностей геометрии того или иного дерева, но в целом зависимость строго соблюдается.

До работы Эллоя основной считалась версия о наличии связи между правилом Леонардо и питанием деревьев. Чтобы объяснить этот феномен, ботаники предположили, что подобное отношение оптимально для работы системы трубок, по которым вода поднимается от корней дерева к листве. Идея выглядит вполне обоснованной хотя бы потому, что от квадрата радиуса прямо зависит площадь сечения, определяющая пропускную способность трубы. Однако французский физик Кристоф Элой (Christophe Eloy) с этим не согласен — по его мнению, связана такая закономерность не с водой, а с воздухом.

Что скрывает число Пи

Число Пи - одно из самых популярных математических понятий. О нем пишут картины, снимают фильмы, его играют на музыкальных инструментах, ему посвящают стихи и праздники, его ищут и находят в священных текстах.

Кто открыл π?

Кто и когда впервые открыл число π, до сих пор остается загадкой. Известно, что строители древнего Вавилона уже вовсю пользовались им при проектировании. На клинописных табличках, которым тысячи лет, сохранились даже задачи, которые предлагали решить с помощью π. Правда, тогда считалось, что π равно трем. Об этом свидетельствует табличка, найденная в городе Сузы, в двухстах километрах от Вавилона, где число π указывалось как 3 1/8 .

В процессе вычислений π вавилонцы обнаружили, что радиус окружности в качестве хорды входит в нее шесть раз, и поделили круг на 360 градусов. А заодно сделали то же самое с орбитой солнца. Таким образом, они решили считать, что в году 360 дней.

• В Древнем Египте π было равно 3,16.
• В древней Индии – 3,088.
• В Италии на рубеже эпох считали, что π равно 3,125.

В Античности самое раннее упоминание π относится к знаменитой задаче о квадратуре круга, то есть о невозможности при помощи циркуля и линейки построить квадрат, площадь которого равна площади определенной окружности. Архимед приравнивал π к дроби 22/7.

Ближе всего к точному значению π подошли в Китае. Его вычислил в V веке н. э. знаменитый китайский астроном Цзу Чунь Чжи. Вычислялось π довольно просто. Надо было дважды написать нечетные числа: 11 33 55, а потом, разделив их пополам, поместить первое в знаменатель дроби, а второе – в числитель: 355/113. Результат совпадает с современными вычислениями π вплоть до седьмого знака.

Почему π – π?

Сейчас даже школьники знают, что число π - математическая константа, равная отношению длины окружности к длине её диаметра и равняется π=3,1415926535 … и далее после запятой – до бесконечности.

Свое обозначение π число обрело сложным путем: сначала этой греческой буквой в 1647 году математик Уи́льям О́тред обозвал длину окружности. Он взял первую букву греческого слова περιφέρεια — «переферия». В 1706 году английский преподаватель Уильям Джонс в работе «Обозрение достижений математики» уже называл буквой π отношение длины окружности к ее диаметру. А закрепил название математик XVIII века Леонард Эйлер, перед авторитетом которого остальные склонили головы. Так π стало π.

Фрактал Мандельброта

Фракта́л (лат. fractus — дроблёный, сломанный, разбитый) — геометрическая фигура, обладающая свойством самоподобия, то есть составленная из нескольких частей, каждая из которых подобна всей фигуре целиком. В математике под фракталами понимают множества точек в евклидовом пространстве, имеющие дробную метрическую размерность (в смысле Минковского или Хаусдорфа), либо метрическую размерность, отличную от топологической.

Впервые множество Мандельброта было описано в 1905 году Пьером Фату (Pierre Fatou), французским математиком, работавшим в области аналитической динамики комплексных чисел. Фату никогда не видел изображений, которые мы сейчас знаем как изображения множества Мандельброта, потому что необходимое количество вычислений невозможно провести вручную. Профессор Бенуа Мандельброт был первым, кто использовал для этого компьютер.

Фракталы были описаны Мандельбротом в 1975 году в его книге «Les Objets Fractals: Forme, Hasard et Dimension» («Фрактальные объекты: форма, случайность и размерность»). В этой книге Мандельброт впервые использовал термин «фрактал» для обозначения математического феномена, демонстрирующего столь непредсказуемое и удивительное поведение.

Douady и Hubbard доказали, что множество Мандельброта является связным, хотя в это и трудно поверить, глядя на хитрые системы мостов, соединяющие различные его части.

Поиск красивых изображений множества Мандельброта — интересное хобби для очень многих людей. Они собирают коллекции таких изображений, причём каждое из них может быть описано небольшим количеством параметров, например, просто координатами центра.

Фрактал Мандельброта прост в построении. Поэтому все оптимизации вычислений испытывают именно на НЁМ. Такие методы как periodicity checking, boundary tracing или perturbation theory были зачаты именно в этом фрактале. И только позже они вводились в более сложные фракталы с более сложными формулами для их построения!

Этот фрактал поначалу кажется просто непредсказуемым. И, хотя некоторым он кажется обычным и однообразным, я Вас уверяю, что в нём можно найти куда более красивые места! (Если, конечно, вы их исследуете в новейших программах - Kalles Fraktaler и Mandel Machine.) В них-то вы и увидите невообразимый прирост скорости за счёт perturbation theroy, а в Mandel Machine есть даже низкоуровневая оптимизация, включая инструкции SSE и AVX.

Задачи с подвохом | Логические задачи и головоломки

Книга Николая и Павла Полуэктовых

«Озадачник: 133 вопроса на знание логики, математики и физики»

Книга Николая и Павла Полуэктовых «Озадачник: 133 вопроса на знание логики, математики и физики».

Изначально это была настольная игра: условия задачи, три варианта ответа и решение, чтобы свериться. По тому же принципу устроена и книга.

В данном посте выбраны семь логических задач, которые помогут понять, как изобретение касок увеличило количество раненых солдат и что ответить на смертной казни, чтобы избежать наказания.

О книге

Михаил Левандовский

В книге «Озадачник» радость узнавания вас ждет уже в первой части — логике. Все то, на чем тренируется хорошая команда «Что? Где? Когда?» в начале своей карьеры, здесь. Многие логические задачки и не задачки, конечно, а старые добрые загадки, некоторые почти со столетней историей, но так приятно увидеть их снова и вместе.

Задачи по математике и физике — сложнее. Вы могли с ними уже встречаться на страницах учебников (задания с повышенной сложностью) или журнала «Квант». С учетом того, что все они из разных разделов, получается довольно интересное блюдо в стиле фьюжен.

Пригодится всем, кто когда-то знал, но забыл. А еще книга будет очень полезна для родителей — многие из этих задач приятно решать вместе с детьми. В общем, правильная книжка, рекомендую.

Михаил Левандовский,
трижды чемпион мира по "Что? Где? Когда?"

Может ли завтра начаться сегодня? Как быстро перемножить в уме 748 на 1503? Каков минимальный размер черной дыры? Почему не тают ледяные жилища эскимосов, когда в них разводят огонь? Авторы предлагают вам проверить свои знания математики, физики и логики. Каверзные вопросы, варианты ответов с подвохом и подробные решения помогут провести время интересно и с пользой.

Орел или решка?

Монета выпадает орлом или решкой с одинаковой вероятностью ½ (50%). В эксперименте подбросили монету 10 раз и — чудеса! — все 10 раз выпал орел. Какова вероятность, что и на одиннадцатом броске снова выпадет орел?

Варианты ответов

1) ½ (50%). 2) ½ в 11-й степени (0,0005, или 0,05%), практически невероятное событие. 3) Определяется временем между бросками: если подождать достаточно долго, то события будут независимыми, и вероятность составит 50%; если бросить сразу, то вероятность 11 раз подряд получить орла — 0,05%. Правильный ответ: 1 Интуиция подсказывает, что не может 11 раз выпадать орел и, значит, вероятность его появления после того, как он выпал 10 раз подряд, должна быть ниже, чем при первом броске. Увы, интуиция нас подводит — она не ниже, а такая же, всегда 50%. Предыстория процесса на нее никак не влияет. Это, кстати, никак не доказывается, а принимается на веру — есть такая эргодическая гипотеза, которую можно сформулировать и так: подбрасывание одной монеты n раз подряд и одновременное подбрасывание n монет со статистической точки зрения совершенно эквивалентны. Когда мы подбрасываем n монет, они уж точно друг о друге ничего не «знают» и выпадают орлом или решкой с вероятностью 50% (для каждой). Эргодическая гипотеза не доказывается, но при этом безупречно работает в статистике, термодинамике, квантовой физике и т. д. Так что вероятность выпадения орла на 11-м броске остается той же самой — другое дело, что оказаться в реальности, когда перед этим 10 раз подряд выпал орел (или 10 раз подряд выпало «красное» на рулетке, или 10 раз подряд выиграть в техасский покер с двумя двойками и т. п.), крайне маловероятно — 0,1%. В среднем такой результат будет получаться в одном эксперименте из тысячи.

Казнить нельзя помиловать

Суд в одной из ближневосточных стран приговаривает преступника к смертной казни. По законам этой страны приговоренный имеет право на последнее слово, которое может содержать не более одного утверждения. Если оно будет истинным, преступника утопят, если же ложным — тогда повесят. Осужденный произносит одну фразу, после чего казнь немедленно отменяют. Что же такого он сказал?

Варианты ответов

1) «Меня повесят».
2) «Меня не повесят, но утопят».
3) «Меня не повесят и не утопят».
Правильный ответ: 1
Произнеся «Меня повесят», преступник поставил суд в безвыходное положение. Если утверждение истинно и его и правда повесят, то нарушат закон, так как в этом случае осужденного должны были не вешать, а топить. Если же оно ложно, то его не могут ни утопить (топят только тогда, когда утверждение истинно), ни повесить (потому что тогда оно перестанет быть ложным). Чтобы не нарушить закон, судья вынужден отменить казнь.
Рассуждая аналогично, нетрудно показать, что фразы «Меня повесят, но не утопят» и «Меня не утопят» приведут к такому же результату.

Библейская загадка о мерах зерна и воздаянии для ученых

Физики и математики из Австралии ищут способ максимально плотно упаковывать зерна пшеницы, вытянутые капсулы лекарств или наночастицы, последовав тем самым притче о воздаянии из Библии.

«В Евангелии от Луки есть следующая строчка:

«Давайте, и дастся вам: мерою доброю, утрясенною, нагнетенною и переполненною отсыплют вам в лоно ваше; ибо какою мерою мерите, такою же отмерится и вам».

Этот стих упоминает все те вещи, которые мы делали в лаборатории: сжимали, трясли и отсыпали. Конечно, я не уверен, что авторы Библии имели в виду то же самое, что и мы ... » — шутит Мохаммед Саадатфар (Mohammad Saadatfar) из Национального университета Австралии в Канберре.

Тем не менее, признает физик, Библия поставила одну из главных и пока не решенных задач математики, физики и химии — то, как можно разместить зерна пшеницы или любые другие продолговатые структуры, чтобы они были максимально плотно и прочно упакованы

Решение этой задачи необходимо, в частности, для того, чтобы наиболее эффективно перевозить грузы, строить более прочные здания из песка и распределять наночастицы по материалам будущего.

Природа, как рассказывают учёные, давно решила эту задачу для кристаллов и сплавов — в их кристаллических решетках атомы упакованы максимально плотно. К примеру, атомы хлора и натрия в кристаллах обычной поваренной соли занимают свыше 74% пространства благодаря упаковке в так называемый гранецентрированный куб.

Интерактивная онлайн-доска Everyday Mathematics

Интерактивная онлайн-доска Everyday Mathematics

На сайте сообщества учителей Intel Education Galaxy написана интересная заметка: "Математическая доска online и ее инструменты".

Инструмент, о котором идет речь, расположен на сайте everydaymath.com. Хотя это только лишь демонстрационная версия коммерческого продукта, который предлагает проект Everyday Mathematics, ее возможности можно с успехом использовать не только на уроках математики.

Сколько всего фотонов во Вселенной?

Фотоны — элементарные безмассовые частицы, кванты электромагнитного излучения, которые мы воспринимаем как свет. Множество фотонов попадают на окружающие нас предметы и отражаются в сетчатку нашего глаза, давая нам возможность видеть.

Казалось бы, подсчитать количество фотонов во Вселенной — задача невозможная. Но как бы то ни было, профессор физики Тони Падилла из Нотингемского университета разработал способ оценки общего количества частиц во Вселенной, не принимая в расчет фотоны или нейтрино, поскольку у них отсутствует (вернее, практически отсутствует) масса:

Учитывая, что приблизительно 5 триллионов атомов водорода могут поместиться на одной лишь головке булавки, при этом каждый из них состоит из 4 элементарных частиц (1 электрон и 3 кварка в протоне), можно с уверенностью предположить, что число частиц в наблюдаемой Вселенной находится за гранью человеческого представления.

Для своих расчетов ученый использовал данные, полученные с помощью телескопа Планка, которые использовались для измерения реликтового излучения, являющегося самым старым из видимого светового излучения во Вселенной и, таким образом, формирующего подобие ее границы. Благодаря телескопу, ученые смогли оценить плотность и радиус видимой Вселенной.

Другая необходимая переменная — это доля вещества, содержащаяся в барионах. Эти частицы состоят из трех кварков, и наиболее известными барионами на сегодняшний день являются протоны и нейтроны, а потому в своем примере Падилла рассматривает именно их. Наконец, для расчета необходимо знание масс протона и нейтрона (которые примерно совпадают друг с другом), после чего можно приступать к вычислениям.

Что делает физик? Он берет плотность видимой Вселенной, умножает ее на долю плотности одних лишь барионов, а затем умножает результат на объем Вселенной. Получившуюся в результате массу всех барионов во Вселенной он делит на массу одного бариона и получает общее количество барионов. Но барионы нам не интересны, наша цель — элементарные частицы.

Собор Тьюринга: от архитектуры фон Неймана к вселенскому разуму Google

Один из главных эпизодов научно-технической революции случился в 1945 году, когда математик Джон фон Нейман, вооружившись идеями Алана Тьюринга, описал принцип работы первого цифрового компьютера и тем самым навсегда изменил мир. Историк науки Джордж Дайсон в эссе «Собор Тьюринга» рассуждает о том, сильно ли эволюция вычислительной архитектуры влияет на человечество, как искусственный интеллект даст знать о том, что он действительно создан, и стоит ли этого бояться.

В цифровой вселенной есть две разновидности битов: те, что образуют собой структуру, находясь в разных частях пространства, и те, что образуют последовательность, меняясь с ходом времени. По определению, данному Аланом Тьюрингом и реализованному Джоном фон Нейманом, цифровая вычислительная машина — это устройство, осуществляющее взаимодействие между двумя разновидностями битов по заданным правилам.

В середине сороковых XX века математик Джон фон Нейман, сотрудник Института перспективных исследований в Принстоне, приступил к поиску средств на создание машины, которая осуществляла бы такое взаимодействие со скоростью перемещения электрического заряда.

«Я абсолютно уверен, что задуманное устройство — вернее, тот класс устройств, который оно представляет пока в единственном числе — окажется настолько революционным, что многие сферы его применения станут понятны только после того, как оно заработает, — писал он Льюису Страуссу 24 октября 1945 года. — По определению, наиболее важными будут те сферы, о которых мы пока и не догадываемся, поскольку они находятся за пределами нашего нынешнего знания».

Фон Неймана немедленно поддержали армия, флот и ВВС США, но главным спонсором выступила Комиссия по атомной энергии (КАЭ). Сделка с дьяволом оказалась уж очень заманчивой. В 1951 году была запущена машина с 5 килобайтами оперативной памяти — матрицей двоичных цифр размерностью 32×32×40. Они были представлены пульсирующей мозаикой электрических зарядов, меняющихся со скоростью миллисекунд на сорока катодно-лучевых трубках.

Архитектура этой пустынной вселенной строилась на следующем принципе: пара 5-битных координат идентифицирует адрес ячейки памяти со строкой в 40 бит. Эти 40 бит могли содержать не только данные (числа, нечто означающие), но и команды (числа, нечто делающие) — например, способные переадресовать задачу другой ячейке или совершить что-то еще.

Упразднив различие между данными и командами, фон Нейман высвободил мощный потенциал компьютеров с запоминаемыми программами и тем самым необратимо изменил наш мир. Неслучайно цепная реакция команд и адресаций в ядре компьютера напоминает цепную реакцию в атомной бомбе.

В начале 1950-х время бесперебойной работы оперативной памяти измерялось считанными минутами. Невозможно было представить, чтобы система, для работы которой критически важна доставка каждого бита в точно определенное ему место и в точно определенное время, стала в 1013 раз больше и заработала в миллион раз быстрее. Фон Нейман очень хотел понять, как природе удается из ненадежных деталей строить надежно функционирующие живые организмы. Он не сомневался, что на смену «архитектуре фон Неймана» вскоре придет какая-то иная. Ведь даже если полностью исключить программные ошибки, никогда нельзя будет полагаться на то, что многие миллионы ячеек памяти станут работать абсолютно бесперебойно.

Спустя пятьдесят лет, благодаря полупроводниковым технологиям, по-прежнему используется именно первоначальная модель фон Неймана. Основная задача компьютерных технологий сейчас не в том, чтобы добиться надежного результата с ненадежным оборудованием, а в том, как обеспечить надежность при использовании недостаточно надежных программ. Архитектура фон Неймана никуда не исчезнет. Но уже появляются новые разновидности архитектуры, содержащие внутри себя привычные машины Тьюринга-фон Неймана. Что же будет дальше? Что представлял фон Нейман перед тем, как остановилась программа его собственной жизни?

Будучи живыми организмами, мы обладаем двумя хранилищами информации: генетической и собранной в нашем мозге. Архитектура того и другого хранилища отлична от фоннеймановской — неудивительно, что это привлекло внимание ученого, когда он намечал программу дальнейших исследований (осуществить которую ему помешал рак). О мозге, как о хранилище информации, он писал в опубликованной посмертно книге «Компьютер и мозг». В языке, используемом нервной системой, меньше логической и арифметической глубины, чем в привычных нам языках, он должен принципиально от них отличаться по своей структуре».

Или, как выразился друг фон Неймана Станислав Улам:

«С чего вы взяли, что мы мыслим в согласии с законами математической логики?» 

Частотное кодирование, которое наблюдается в нервной системе и используется в основанных на вероятностных моделях поисковых машинах, зависит не от точных характеристик данных, а от связей между ними и статистики частоты их использования. Фон Нейман писал в 1948 году:

«Для того, чтобы понять, как функционируют высокосложные устройства и, в частности, центральная нервная система, необходима новая теория, основанная на базе логики. Однако по ходу создания такой теории логике с гораздо большей вероятностью грозит пережить трансформацию в неврологию, чем неврологии — в логику».

Смерть фон Неймана совпала с началом революции в микробиологии, вспыхнувшей после того, как в 1953 году была раскрыта структура ДНК. Жизнь в современном понимании основана на представленных в цифровом коде командах, которые преобразуют последовательность в структуру (от нуклеотидов до белков) в точном соответствии с определением Тьюринга. Рибосомы и прочая клеточная машинерия выполняют роль программы: считывают, дуплицируют и интерпретируют записанные на ленте последовательности. Как ни поразительно сходство, не следует забывать, что для исполнения команд в живой и электронной системах используются абсолютно разные способы адресации.

Почему мы ещё не встретили инопланетян: самые правдоподобные объяснения парадокса Ферми

Москва получает новейшее оружие от инопланетян,

США "бессильны" 😊😊😊

«Где они?» — поинтересовался в 1950 году итальянский физик Энрико Ферми, разговаривая с коллегами. И хотя вопрос прозвучал вне контекста, собеседники учёного сразу поняли, что он имеет в виду инопланетян. Сомнения Ферми были обоснованными: Млечный Путь существует 13,2 млрд лет, в нём есть около 200 млрд звёздных систем, примерно в 10 % этих систем есть планеты, похожие на Землю, а значит, люди, по идее, давно должны были встретить инопланетный разум или хотя бы признаки того, что он существует (или существовал). Здесь собраны самые правдоподобные объяснения, почему этого до сих пор не произошло.

Людям очень повезло,  что они существуют

Хотя потенциально есть миллиарды планет, похожих на Землю, разумная жизнь (да и жизнь в принципе) — очень хрупкая штука, считают некоторые учёные. Её становление заняло около четверти общего возраста Вселенной: так, одноклеточным бактериям потребовалось 1,7 млрд лет, чтобы развиться до сложных. Всё это время эволюция будто стояла на месте, и любой космический катаклизм рядом с Солнечной системой мог уничтожить простейшие земные организмы. Более того, старея, звёзды светят всё ярче, из-за чего климат на планетах становится непригодным для углеродных организмов. Но на Земле сложилась уникальная обстановка: хотя Солнце греет её всё сильнее, геологические и биологические процессы постоянно её охлаждают, а потому температура всегда колебалась не так сильно, как могла бы.

Именно эти тепличные условия могли дать жизни на Земле преодолеть так называемый «Великий фильтр» — гипотетическое препятствие, которое не позволяет жизни возникать и колонизировать галактики. Концепцию Великого фильтра изобрёл экономист Робин Хэнсон, задавшийся вопросом, когда мы его преодолеем и сможем ли это сделать вообще. Великий фильтр может стать как хорошим, так и плохим известием для человечества. Хорошим, как говорит философ Ник Бостром, в том случае, если мы уже его прошли (хотя это и снизит наши шансы встретить внеземной разум), плохим — если он ещё впереди, а значит, мы можем исчезнуть, так и не обнаружив решение парадокса Ферми (а точнее — не успев его осознать).

Краткая история числа «Пи»

С тех пор, как у людей появилась возможность считать и они начали исследовать свойства абстрактных объектов, называемых числами, поколения пытливых умов совершали завораживающие открытия.

По мере того как наши знания о числах увеличивались, некоторые из них привлекали особое внимание, а некоторым даже придавали мистические значения.

Был 0, который обозначает ничего, и который при умножении на любое число дает себя.

Была 1, начало всего, также обладающая редкостными свойствами, простые числа.

Затем обнаружили, что существуют числа, которые не являются целыми, а иногда получаются в результате деления двух целых чисел, — числа рациональные.

Иррациональные числа, которые не могут быть получены как отношение целых чисел, и т.д.

Но если и есть число, которое очаровало и вызвало написание массы трудов, то это "пи": число, которое, несмотря на долгую историю, не называли так, как мы называем его сегодня, до восемнадцатого века.

Начало

Число "пи" получается делением длины окружности на ее диаметр. При этом размер окружности не важен. Большая или маленькая, отношение длины к диаметру одно и то же.

Хотя вполне вероятно, что это свойство было известно ранее, самые первые свидетельства об этом знании — Московский математический папирус 1850 г. до н.э. и папирус Ахмеcа 1650 г. до н.э. (хотя это копия более старого документа). В нем имеется большое количество математических задач, в некоторых из которых "пи" приближается как 256/81, что чуть более чем на 0,6% отличается от точного значения.

Примерно в это же время вавилоняне считали "пи" равным 25/8.

В Торе, написанной более десяти столетий спустя, Яхве не усложняет жизнь и божественным указом устанавливает, что "пи" в точности равно 3.

Однако великими исследователями этого числа были древние греки, такие как Анаксагор, Гиппократ из Хиоса и Антифон из Афин.

Ранее значение "пи" определялось, почти наверняка, с помощью экспериментальных измерений. Архимед был первым, кто понял, как теоретически оценить его значение.

Использование описанного и вписанного многоугольников (больший описан около окружности, в которую вписан меньший) позволило определить, что "пи" больше 223/71 и меньше 22/7.

С помощью метода Архимеда другие математики получили лучшие приближения, и уже в 480 г. Цзу Чунчжи определил, что значения "пи" находится между 3,1415926 и 3,1415927.

Тем не менее метод многоугольников требует много вычислений (напомним, что все делалось вручную и не в современной системе счисления), так что у него не было будущего.

Представления

Нужно было дождаться XVII века, когда с открытием бесконечного ряда свершилась революция в вычислении "пи", хотя первый результат не был рядом, это было произведение.

Бесконечные ряды — это суммы бесконечного числа членов, образующих некоторую последовательность (например, все числа вида 1/n, где n принимает значения от 1 до бесконечности).

Во многих случаях сумма конечна и может быть найдена различными методами.

Оказывается, что некоторые из этих рядов сходятся к "пи" или некоторой величине, имеющей отношение к "пи".

Очевидное — недоказуемое, или Почему теоремы Гёделя о неполноте волнуют не только математиков

Ну, предположим, ква…

Как развивается научная модель в естественных науках? Накапливается житейский либо научный опыт, его вехи аккуратно формулируются в виде постулатов и образуют базу модели: набор утверждений, принимаемых всеми, кто работает в рамках этой модели.

Новые исследования и добытые в них знания могут поколебать набор утверждений, принимаемых в качестве бесспорных, и, если к тому появляются основания, какие-то утверждения заменяются на новые. Например, когда на пороге ХХ века началось развитие физики в области, выходящей за пределы привычного мак-ромира, был сформулирован постулат о том, что скорость света предельна, больше её скоростей не бывает.

Постулаты реальной науки — результат большой и длительной работы по накоплению знаний. Их невозможно доказать абсолютно, но в конкретный момент они лучше всего подходят для описания наблюдаемой реальности и не вызывают явных противоречий. Если мы исходим из того, что яблоко падает с ветки на землю, а не улетает куда угодно, то мы принимаем закон всемирного тяготения, хотя доказать его в абсолютном, логическом смысле слова далеко не просто, если вообще возможно.

Теорема Гёделя — это математическое утверждение, сделанное относительно одного конкретного инструмента познания — логики.

Любую логику задают три структурных элемента: её алфавит, утверждения и правила вывода.

Алфавит — это, например, символы переменных (A, B, C…), которые принимают различные значения, и кванторы существования и общности. С их помощью можно строить утверждения, например такое: «Любой дедушка — мужчина» («(любое) х, принадлежащее множеству Х, принадлежит также его множеству Y», где х — человек, Х — множество мужчин, имеющих внуков, а Y — множество всех мужчин).

YouTube-канал с визуализацией математических теорий

Фракталы

Для производства роликов автор канала (студент факультета математики в Стэнфорде Грант Сандерсон) использует язык программирования Python, программы Final Cut Pro и Grapher.

Сандерсон также ведет собственный сабреддит, где отвечает на вопросы о математике и помогает решать сложные задачи, — подойдет тем, кто увлечен уравнениями всерьез.

Как устроена структура фракталов,
линейная алгебра и блокчейн —
в понятных картинках и графиках

3Blue1Brown

Все видеоматериалы

(Нажми) 😊

Червоточины

«Интерстеллар. Наука за кадром»

Кип Торн

Глава из книги «Интерстеллар. Наука за кадром» американского физика-теоретика и астронома, профессора Калифорнийского технологического института Кипа Торна, посвященной его опыту работы в качестве научного консультанта над фильмом “Interstellar” (реж. Кристофер Нолан, 2014).

Рассказывая по ходу этой книги о каком-либо явлении в «Интерстеллар», я указываю его статус (научная истина, обоснованное предположение или домысел), помещая в начале главы или параграфа один из значков:

(И) — истина

(ОП) — обоснованное предположение

(Д) — домысел

Откуда взялось название «червоточина»

(И)

Название астрофизическим червоточинам придумал мой научный руководитель Джон Уилер.

Он использовал сравнение с червоточинами в яблоках (рис. 14.1). Для муравья, который ползает по яблоку, поверхность яблока — это целая вселенная. Если плод насквозь проеден червем, муравей может попасть с верхней части яблока на нижнюю двумя способами: проползти снаружи (через свою вселенную) или спустившись по червоточине. Путь через червоточину короче, это способ срезать дорогу, быстрее попав с одной стороны муравьиной вселенной на другую.

Рис. 14.1. Муравей исследует яблоко с червоточиной

Аппетитная мякоть яблока, через которую проходит червоточина, не относится к муравьиной вселенной. Это трехмерный балк, или гиперпространство (см. главу 4). С одной стороны, стенки червоточины можно считать частью муравьиной вселенной — их поверхности имеют одну и ту же мерность (два измерения) и смыкаются со вселенной (с поверхностью яблока) на входе в червоточину. Но с другой — стенки червоточины не принадлежат муравьиной вселенной, это просто короткий путь через балк, по которому муравей может попасть из одной точки своей вселенной в другую.

Червоточина Фламма

(И)

В 1916 году, всего через год после того, как Эйнштейн сформулировал законы общей теории относительности, Людвиг Фламм из Вены нашел решение уравнений Эйнштейна, которое описывает червоточину (хоть Фламм ее так и не называл). Сейчас мы знаем, что уравнения Эйнштейна допускают существование червоточин разной формы и разных свойств, но червоточина Фламма — единственная из них в точности сферическая и не содержащая гравитирующей материи.

Если мы сделаем экваториальный срез червоточины Фламма, так чтобы и она, и наша Вселенная (наша брана) имели два измерения вместо трех, а затем посмотрим на нашу Вселенную и на червоточину из балка, то они будут выглядеть как показано на левой части рис. 14.2.

Поскольку одно из измерений нашей Вселенной на этом рисунке отсутствует, вам следует думать о себе как о двумерном существе, перемещения которого ограничены поверхностью изогнутого «листа» или двумерных стенок червоточины. Есть два способа попасть из пункта A нашей Вселенной в пункт B: короткий путь (синий пунктир) по стенке червоточины и длинный путь (красный пунктир) по поверхности «листа» нашей Вселенной.

Разумеется, пространство нашей Вселенной трехмерно, а не двумерно. И концентрические окружности на левой части рис. 14.2 — это на самом деле вложенные одна в другую зеленые сферы, показанные на правой части рисунка. Войдя в червоточину и двигаясь по идущему от точки А синему пунктиру, вы будете проходить через сферы всё меньшего и меньшего размера.

Затем сферы, хоть они и вложены одна в другую, перестанут менять размер. А потом, по мере того как вы будете выбираться из червоточины, приближаясь к точке B, величина сфер начнет расти.

Рис. 14.2. Червоточина Фламма

В течение девятнадцати лет физики почти не обращали внимания на экстравагантный вывод из уравнений Эйнштейна, предложенный Фламмом, — на его червоточину. Затем в 1935 году сам Эйнштейн и его коллега, физик Натан Розен, не зная о работах Фламма, самостоятельно пришли к тому же выводу, в подробностях исследовали его и принялись размышлять о его значимости для реального мира. Другие физики, также не зная о решении Фламма, стали называть его червоточину мостом Эйнштейна — Розена.

Схлопывание червоточины

(И)

Зачастую из уравнений эйнштейновской теории сложно понять, что, собственно, из них следует. Червоточина Фламма — хороший тому пример. С 1916 до 1962 года, почти полвека, физики считали, что червоточины статичны, никогда не меняются. Затем Джон Уилер и его студент Роберт Фуллер выяснили, что это не так. Пристально изучив уравнения, они обнаружили, что червоточины рождаются, расширяются и умирают, как показано на рис. 14.3.

Сначала (а) в нашей Вселенной есть две сингулярности. Со временем сингулярности сближаются через балк и, встретившись, образуют червоточину (b). Червоточина расширяется (c, d), а потом сжимается (e) до тех пор, пока не схлопнется, разделившись на две сингулярности (f). Рождение, расширение, сжатие и схлопывание происходят очень быстро, и ничто — даже свет — не успевает проникнуть по червоточине с одной стороны на другую.

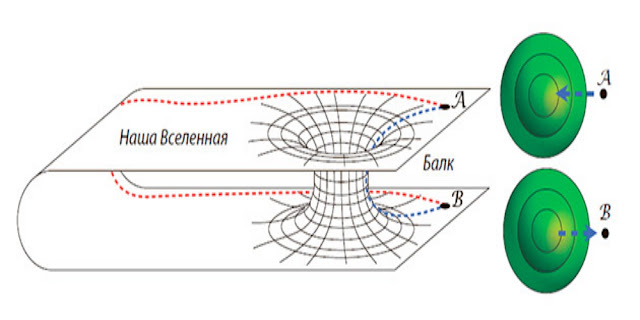
Рис. 14.3. Динамика червоточины Фламма (моста Эйнштейна — Розена)

(Рисунок Мэтта Зимета по моему наброску; из книги [Торн 2009].)

Такой ход событий неизбежен. Если бы во Вселенной когда-либо, каким-либо образом возникла сферическая червоточина, не содержащая гравитирующей материи, она, согласно законам теории относительности, вела бы себя именно так.

Наука о волшебных свойствах числа семь

Волшебные свойства числа семь известны с детства из сказок. Но народ неслучайно выбрал именно его. Психологические эксперименты показали, что эта цифра имеет для людей ключевое значение — в семерках измеряется объем нашего сознания.

Сегодня это кажется странным, но еще каких-то 150 лет назад для изучения столь тонких субстанций, как душа или сознание, ученые располагали богатым арсеналом всего из двух инструментов. Психологи позапрошлого столетия либо «обращали сознание на себя», то есть попросту медитировали, либо пространно рассуждали на интересующую их тему.

Так продолжалось до тех пор, пока в последней трети XIX века на научную сцену не вышел профессор Лейпцигского университета Вильгельм Вундт, который первым решил проверить психологические гипотезы экспериментально и превратил психологию из любопытной концепции в науку.

Даже по тем пуританским временам Вундт был на редкость скучным человеком: все в его жизни было строго регламентировано — работа, общение с семьей, досуг. По воспоминаниям жены ученого Софи, он придерживался одного и того же распорядка: утром писал, днем посещал сотрудников в лаборатории (не более 10 минут на каждого), затем прогулка и лекция, вечером — прием гостей, музицирование и разговоры о политике.

Но именно эта педантичность подняла психологию на новую высоту — скучный профессор методично и размеренно внедрил в нее экспериментальные методы.

ЭКСПЕРИМЕНТ
Осмыслить абракадабру
Каждый человек может легко убедиться в способности сознания группировать элементы.
Легко ли вы запомните эти буквы в нужной последовательности?
МУРМЧСКПКТНТ
А если так?
МУР МЧС КПК ТНТ
Разделенные на смысловые группы, стимулы запоминаются гораздо лучше. Отличный пример подобной группировки продемонстрирован в известной песне Бориса Гребенщикова.
2-12-85-06 — Запоминается?
2128506 — А в этой строчке вы бы узнали телефон?

Искусственный естественный лес

Думаю, все читатели согласятся, что природу нужно охранять, помогать ей залечивать раны, нанесённые человеком. Например, если где-то вырубили лес, нужно вырастить его заново. Причём желательно, чтобы вырос именно такой лес, какой существовал задолго до появления человека с топором и пилой, — естественный, или, как говорят ботаники, коренной. Хотя бы потому, что естественные природные сообщества более устойчивы.

Искусственное сообщество, например клумба с розами или картофельное поле, может быть очень красивым и полезным, но само себя поддерживать не способно — зарастает «сорняками» и очень быстро превращается в заросли бурьяна, а потом просто в луг или лес. Чтобы розарий остался розарием, его нужно пропалывать, поливать, удобрять, укрывать на зиму и много чего ещё делать. А леса миллионы лет живут безо всякой прополки.

Всё это так, но где сейчас найти естественные леса? Понятно, что посаженные рядочками ели — это искусственное сообщество. И потому не очень устойчивое: стоит случиться жаркому сухому лету, как в нём массово размножаются короеды, и большая часть елей погибает.

Но вот обширный сосняк, который явно никто не сажал: деревья растут хаотично, причём растут уже много поколений. На месте умерших от старости сосен вырастают их «дочки», затем их сменяют «внучки», «правнучки»... Устойчивое сообщество? Ещё какое! Значит, естественное, коренное? А вот и нет!

Хотя ещё недавно даже серьёзные учёные-лесоведы считали сосняки коренным типом леса: трудно было представить себе, что столь обширные леса возникли не сами, а по вине людей. Да в них кое-где лет сто «не ступала нога человека»! Как же они могут быть неестественными?!

Чтобы ответить на этот вопрос, нужно выяснить, как живёт сосна и что ей нужно от жизни. Так вот, оказывается, сосна — очень «слабое» дерево, проигрывающее в конкуренции всем другим видам. Во-первых, она ужасно светолюбива — молодые сосенки могут вырасти только на открытом месте: на поляне, вырубке, пожарище и т. п. 

 

Само по себе это не страшно — мы помним, что у светолюбивых деревьев есть свои сильные стороны. Но, как мы выяснили, всем, кто слишком любит свет, нужно иметь много лёгких, далеко разлетающихся семян — иначе не получится быстро заселить «освободившиеся» места в лесу. А у сосны и семян не так много, как у берёзы или осины, и распространяются они не столь далеко — тяжеловаты.

При этом у сосны слабые проростки, с трудом пробивающиеся сквозь траву — значит, она медленно заселяет луга с густым травостоем. Да и светолюбие сосны просто зашкаливает: ей требуются очень крупные «окна», в то время как другие светолюбивые деревья готовы вырастать и в относительно небольших. Посмотрите на лесной поляне, просеке, вырубке — молодые берёзки и осинки вы найдёте с лёгкостью, а вот сосенки нужно ещё поискать. Даже при том, что взрослые деревья, производящие семена, — вот они, рядом.

Да и растут молодые сосны не так уж и быстро, а это светолюбивому дереву и вовсе противопоказано: стоит немного отстать в росте — и всё, попадёшь в тень более удачливых конкурентов и погибнешь.

Математическое доказательство размером с Википедию

Компьютер частично разрешил математическую проблему, выдав доказательство более чем на 15 тысяч страниц — перепроверить его вручную невозможно. Это поднимает вопрос об исключении человека из математики, пишет (перевод из их статьи самого главного).

Если в школе разбор доказательств к теоремам и так казался пыткой, то теперь представьте, что вам пришлось столкнуться с доказательством размером с Википедию. Исследователи компьютерных технологий из университета Ливерпуля — Алексей Лисица и Борис Конев — получили математическое доказательство, которое изложено в 13-гигабайтом файле, превышающим все сложенные вместе страницы Википедии. Ручная проверка доказательства не представляется возможной.

Тем не менее, это большой шаг вперед в решении проблемы несоответствия, которая была предложена знаменитым венгерским математиком Палом Эрдешем в 1930-е. характеризует структуру подпоследовательности также, как и всю бесконечную последовательность.

Основная гипотеза Эрдеша состояла в том, что может быть найдено несоответствие любой величины, но он так никогда не смог этого доказать. Ученые решили воспользоваться компьютером, чтобы доказать, что бесконечная последовательность всегда будет иметь несоответствие, равное двум или большему числу. Компьютер потратил на проверку шесть часов и выдал доказательство длиннее Огромной Теоремы, изложенной на 15000 листах.

Проверить этот массив данных для человека не представляется возможным, и если доказательство с расхождением 2 оказалось настолько сложным, значит ручной проверке не пригодны и доказательства с большими расхождениями. Это поднимает вопрос о математике, из которой исключен человек: если доказательство может быть проверено только на компьютере, может ли оно считаться верным? По мнению Джила Калаи из Института математики в еврейском университете в Иерусалиме, исключительно человеческого мозга здесь недостаточно. Но если другой компьютер получит такое же доказательство с теми же результатами, тогда его можно считать верным.

Лисица и Конев уже приступили к следующему проекту — их компьютер остаются включенным на протяжении недель, чтобы найти результат отклонения со значением три.

Подробнее узнать о недоступном для человеческого ума доказательстве проблемы несоответствия можно на сайте Verge.

Фотографии теней

Мне всегда философы казались большими чудаками. Их занимают вопросы, которые, на взгляд нефилософа, кажутся простыми и понятными. Особенно преуспели в этом древнегреческие философы. Их всерьёз занимало, догонит ли Ахиллес черепаху? Или на сколько частей можно разделить яблоко, чтобы яблоко оставалось яблоком?

Когда я учился геометрии в школе, мне казалось, что многие теоремы и так понятны или, как говорят, очевидны. Например, теорема греческого геометра Фалеса, которую мы учились доказывать на уроках.

Теорема Фалеса

Если параллельные прямые, пересекающие стороны угла, отсекают на одной его стороне равные отрезки, то они отсекают равные отрезки и на другой его стороне (рис. 1).

Рис. 1 (слева) и 2

Теорему Фалеса можно применять для деления отрезка на n равных частей (рис. 2, отрезок AB).

Теорема кажется понятной и естественной без доказательства! Как проверить её экспериментально? Давайте в качестве параллельных прямых (секущих) использовать солнечные лучи, в качестве одной стороны угла — поверхность земли, а другой палку с вбитыми на равном расстоянии гвоздями. Мы ожидаем, что тень от гвоздей на земле будет на одинаковом расстоянии. 

Чтобы зарегистрировать результат, мы воспользовались фотоаппаратом, а палку с гвоздями заменили самим фотографом.

Фото 1

Результат эксперимента показан на фотографиях 1 и 2. Это тени фотографа. Тени ног длинноваты! А тень головы определённо маловата. В чём дело? Кто не прав? Фалес или экспериментатор?

Как математик помог биологам совершить важное открытие

Несмотря на то, что математику часто называют фундаментальной наукой, она так же часто не получает достаточного уважения, когда представляют научные открытия. Но вклад математики и статистики крайне важен и преобразовал целые области исследований — многие открытия были бы невозможны без них. Далее — рассказ математика от первого лица.

Несмотря на то, что математику часто называют фундаментальной наукой, она так же часто не получает достаточного уважения, когда представляют научные открытия. Но вклад математики и статистики крайне важен и преобразовал целые области исследований — многие открытия были бы невозможны без них. Далее — рассказ математика от первого лица.

Как математик, я сделал вклад в научные открытия и представил решения проблем, которые пытались решить биологи. Семь лет назад я посетил лекцию на тему биологических исследований, которые проводились в университете Херио-Ватт. У моих коллег была нерешенная проблема, связанная с движением мешкообразных структур, называемых везикулами, которые перемещают гормоны и нейротрансмиттеры, такие как инсулин и серотонин, по клеткам и телу.

Их проблема заключалась в том, что везикулы, как известно, следуют определенным дорожкам по скелету клетки, которые ведут к особым молекулам, которые затем заставляют везикулу высвободить свое содержимое в клетку. Однако, когда сами биологи попытались найти эти дорожки, тех не оказалось на ожидаемых местах.

Важно понимать, как ведут себя (или не ведут) везикулы, потому что они связаны с разными заболеваниями, от диабета до неврологических расстройств. Биологи не могли найти способ понимания этих везикул — но у меня было решение в математическом инструментарии.

Математика лучше биологии?

Через два года совместной работы я сказал коллегам: «Моя модель и компьютерные эксперименты лучше вашего микроскопа!».

Под этим весьма гордым заявлением я имел в виду, что, используя математику для моделирования перемещения молекул по клетке, мы можем спрогнозировать и провести множество экспериментов на компьютере в масштабах меньших и более быстром темпе, чем под микроскопом. Это позволяет нам раскрывать то, что не могут позволить ресурсы биологов, и даже указать нам в направлении целевых молекул для будущего лечения диабета и неврологических расстройств.

Математическая модель позволила нам понять, что движение везикул требует энергии — а математика моделирует его на энергетическом ландшафте. Представим, что везикула — это велосипедист, едущий на велосипеде: ландшафт может иметь ровные и неровные участки, которые требуют больше энергии для их преодоления. Мы хотели проверить, действительно ли везикулы стараются избегать этих холмов.